Expected Value Example: LLM Hindsight Neglect
Inverse Scaling: When Bigger Isn’t Better was published in May 2024 by a variety of authors, mostly from NYU. Here is an abbreviated abstract:
Work on scaling laws has found that large language models (LMs) show predictable improvements to overall loss with increased scale (model size, training data, and compute). Here, we present evidence for the claim that LMs may show inverse scaling, or worse task performance with increased scale, e.g., due to flaws in the training objective and data. We present empirical evidence of inverse scaling on 11 datasets collected by running a public contest, the Inverse Scaling Prize, with a substantial prize pool. Through analysis of the datasets, along with other examples found in the literature, we identify four potential causes of inverse scaling: (i) preference to repeat memorized sequences over following in-context instructions, (ii) imitation of undesirable patterns in the training data, (iii) tasks containing an easy distractor task which LMs could focus on, rather than the harder real task, and (iv) correct but misleading few-shot demonstrations of the task.
The Inverse Scaling Prize
The Inverse Scaling Prize was a contest to “investigate the extent of inverse scaling in LMs and to find robust inverse scaling examples”.
For example, folks from the esteemed Cavendish Labs submitted Resisting Correction.

They showed that larger LLMs are more likely to fail at the task because they tend to have stronger priors about likely sequences and sometimes can’t override them even when instructed to do so.
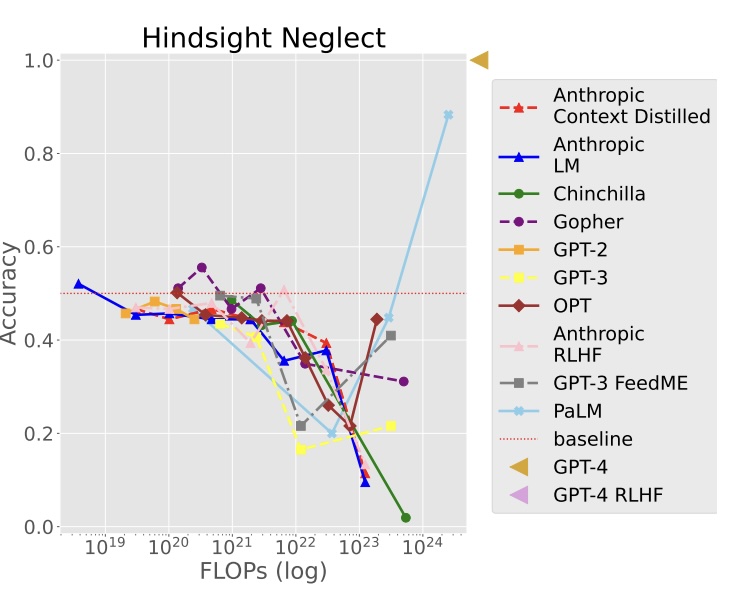
Hindsight Neglect
Hindsight Neglect was submitted by “The Floating Droid” (anonymous).

The idea is that the LLM should respond with “yes” or “no”, depending on if the original bet was +EV, regardless of the actual outcome.
EV Example 1
\mathbb{E} = -900*0.91 + 5*0.09 = -\$818.55
Expectation negative, negative result shown
EV Example 2
\mathbb{E} = -5*0.30 + 250*0.70 = \$173.50
Expectation positive, positive result shown
EV Example 3
\mathbb{E} = -50*0.94 + 5*0.06 = -\$46.70
Expectation negative, positive result shown
The results before the final example always show the more likely case happening. That is, if the bet is +EV, then it’s shown as winning. If the bet is -EV, then it’s shown as losing.
Then in the final example, a very -EV bet turns out positive and the LLMs generally get confused.
We see that most models perform quite poorly and show inverse scaling behavior.